Note: I haven't used Bryce in years; so these tutorials are archived "as is." I can't accept questions, because I don't remember the answers.
This is the math behind a stack of spheres. When you are ready, you can return to the Page 1. (Or, if you finished it before coming here, you can go right on to Page 2.)
 Alright, you math aficionados! We need to find the center of the sphere on top of the stack of three to be able to multi-replicate them, just as we did before. (Think of it as the vectors that we will have to move the sphere.)
Alright, you math aficionados! We need to find the center of the sphere on top of the stack of three to be able to multi-replicate them, just as we did before. (Think of it as the vectors that we will have to move the sphere.)
In order to do that, we need to know its coordinates in space. We already know the X coordinate; it's going to be 1, because it's the radius of one sphere, and we set that up to be 1.
Let's find the Z coordinate next. We know that the point we are looking for, call it a, is equidistant from the centers of the three spheres on the bottom.
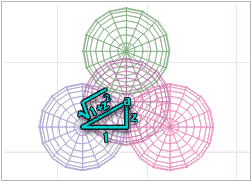 We can draw another right triangle between the center point of the original sphere, on the left, and point a, as shown above. We'll call the length of that triangle on the Z axis z. So, looking at the triangle, we know that the bottom is 1, the right side is z, and the hypotenuse is the square root of the sum of 1 squared + z squared. Since 1 squared is 1, the hypotenuse is the square root of (1+z squared).
We can draw another right triangle between the center point of the original sphere, on the left, and point a, as shown above. We'll call the length of that triangle on the Z axis z. So, looking at the triangle, we know that the bottom is 1, the right side is z, and the hypotenuse is the square root of the sum of 1 squared + z squared. Since 1 squared is 1, the hypotenuse is the square root of (1+z squared).
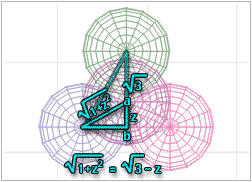 Now, to figure out what z is, all we have to do is remember that the distance from the center of the sphere on the left to point a is the same as the distance from the sphere on the top to point a. If you look at it, you will notice that we have already solved for the length of the line from the center of the top sphere to the bottom of this right triangle at point b; it was the square root of 3, remember?
Now, to figure out what z is, all we have to do is remember that the distance from the center of the sphere on the left to point a is the same as the distance from the sphere on the top to point a. If you look at it, you will notice that we have already solved for the length of the line from the center of the top sphere to the bottom of this right triangle at point b; it was the square root of 3, remember?
So, since the distance from the center from any one sphere to point a is the same as the distance from the center of any of the others to point a, we know that the hypotenuse of the small triangle is equal to the square root of 3 minus z.
Or the square root of (1 + z squared) = (the square root of 3) - z.
 On to the algebra. First, square both sides. You get 1 + z squared = ((the square root of 3) - z) times ((the square root of 3) - z) Expand that, and you get 1 + z squared = 3 - (2 times z times the square root of 3) + z squared.
On to the algebra. First, square both sides. You get 1 + z squared = ((the square root of 3) - z) times ((the square root of 3) - z) Expand that, and you get 1 + z squared = 3 - (2 times z times the square root of 3) + z squared.
The z squared cancels on both sides, giving us 1=3 - (2 * z * sqrt(3)).
Add (2 * z * sqrt(3)) to both sides, and you get 1 + (2 * z * sqrt(3)) =3.
Subtract one from each side, and you get 2 * z * sqrt(3) = 2.
Divide both sides by 2 * sqrt(3) and you get z = 2 / 2 * sqrt(3)
Simplify that, and you get z = 1/sqrt(3) or 1/1.732.
Getting out the handy dandy calculator, we find that z = .5773672. Round it up to .5774 So, the coordinates of point a would be (1, 0, .5774)
 So, the coordinates of point a would be (1, 0, .5774)
So, the coordinates of point a would be (1, 0, .5774)
 Now that we know that, we can find the center of the top sphere. It has the same X and Z coordinates as point a, but an unknown Y coordinate. Let's call that point c. Written in notation, that would be c = (1, Y, 1/sqrt(3)). Now, we want the distance from the center of the sphere on the left to the center of the sphere on top to be 2, like the distances between the centers of all the other spheres.
Now that we know that, we can find the center of the top sphere. It has the same X and Z coordinates as point a, but an unknown Y coordinate. Let's call that point c. Written in notation, that would be c = (1, Y, 1/sqrt(3)). Now, we want the distance from the center of the sphere on the left to the center of the sphere on top to be 2, like the distances between the centers of all the other spheres.
So, we use the 3D version of Pythagoras' theorem, which states that the distance between two points in 3D space is the square root of the sum of the squares of the differences in their coordinates on each axis. In other words, the distance between any two points in space is sqrt(dx squared + dy squared + dz squared) where dx is the difference in their x coordinates, dy is the difference in their y coordinates, and dz is the difference in their z coordinates.
Since the center of the sphere on the left (call it p) is at (0,0,0) these quantities are simply the coordinates of point c; (1, Y, 1/sqrt(3)). (Subtract 0 from a number, and you get the number, of course.)
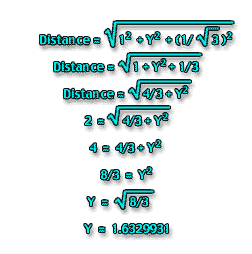 So the distance from the center of the sphere on the left to the center of the sphere on top is sqrt(1 squared + Y squared + (1/sqrt(3))squared). Since 1 squared is 1, and (1/sqrt(3)) squared is 1/3, the distance is the square root of (1+ Y squared + 1/3) or the square root of (4/3 + Y squared.)
So the distance from the center of the sphere on the left to the center of the sphere on top is sqrt(1 squared + Y squared + (1/sqrt(3))squared). Since 1 squared is 1, and (1/sqrt(3)) squared is 1/3, the distance is the square root of (1+ Y squared + 1/3) or the square root of (4/3 + Y squared.)
We want that distance to be 2, so the equation comes out 2 = sqrt(4/3 + Y squared.)
Square both sides, and you get 4 = 4/3 + Y squared.
Subtract 4/3 from both sides, and you get 8/3 = Y squared.
Switch sides and take the square roots, and you get Y = sqrt(8/3).
Grabbing the calculator again, we find that comes out to 1.6329931; call it 1.633.
 The center of that top sphere, then, is at (1, 1.633, .5774). Those numbers form the vector between the center point of the original sphere, (0,0,0) and the one on the top. So all we have to do is plug them into the Multi-Replicate box, and we are all set!
The center of that top sphere, then, is at (1, 1.633, .5774). Those numbers form the vector between the center point of the original sphere, (0,0,0) and the one on the top. So all we have to do is plug them into the Multi-Replicate box, and we are all set!
You can go back to the lesson now, or right on to Page 2 if you already finished the whole first page.